El día de e

Hoy es 7 de febrero y es de justicia hablar de e. Sí, del número e. Y es que hoy, en notación anglosajona, es February 7, es decir, 2.7.

Ingenieros, biólogos, físicos, químicos, matemáticos, paleontólogos, médicos, estadísticos, financieros (as):

Hoy, a lo largo y ancho del mundo, es el día de e.

Mira, te cuento. En realidad, e no es 2.7, sino:

2.7182818284590452353602874713526624977572470936999595749669676277

240766303535475945713821785251664274274663919320030599218174135966

290435729003342952605956307381323286279434907632338298807531952510

190115738341879307021540891499348841675092447614606680822648001684…

Este microrrelato puede ayudarte a recordar sus cifras. Bueno, sólo las veinte primeras…

https://ciencias.ua.es/es/san-alberto-magno-2018/x-concurso-de-microrrelatos-matematicos.html

Vamos a conocerlo un poco mejor…

El número e no tiene ni 20 ni 266 cifras. El número e tiene infinitas cifras. Pero no te asustes, porque sólo es un poooco más grande que 2.7 y, desde luego, más pequeño que 2.8.

Es un número muy especial: irracional, trascendente y normal.

1) El número e es irracional.

Ya sabes que muchos números reales pueden obtenerse a partir de una fracción (por ejemplo, 2.7=27/10). Son los llamados racionales. Pues bien, no hay ninguna fracción que sea equivalente al número e.

2) El número e es trascendente.

Muchos números reales son solución de una ecuación. Por ejemplo, cualquier racional p/q es solución de qx-p=0. O √2 (que es irracional) es solución de x^2-2=0. Pues bien, no hay ninguna ecuación con coeficientes enteros cuya solución sea e. Tela.

3) Se piensa que el número e es normal.

Las cifras de e no siguen ningún patrón, pero se intuye que cada cifra del 0 al 9 aparece en la misma proporción. Si esto se cumpliera, el 1 aparecería el 10% de las veces, y el 2, y el 3… Piensa que esto no se cumple, por ejemplo, en un número tan simple como 2.7777… ¿Quién lo demuestra?

Su primera “aparición” (encubierta) fue en un anexo del trabajo donde John Napier (1614) donde desarrolló los logaritmos. El número e se escondía tras una tabla donde se mostraban los logaritmos neperianos de varios números. Curioso que un número «desconocido» jugara un papel tan crucial, ¿verdad?

Setenta años después, Jacob Bernoulli (1683) estudió el interés compuesto, es decir, el interés monetario sobre una cantidad inicial fija a largo plazo. Jacob reconoció a e como el valor de cierto límite.

Y esto quiero contártelo porque es algo cotidiano. Y porque está guay, vaya

Imagina que ingresas 1€ en una cuenta bancaria a un interés compuesto anual del 100% (situación MUY ficticia, por cierto). Esto quiere decir simplemente que al finalizar cada año doblarás tu capital. Si no empiezas a gastar, que nos conocemos. Jum.

Así, tras el primer año, tendrás 2€; tras el segundo año, 4€; tras el tercero, 8€…

Más generalmente, si tienes en el banco un capital C_0 a un interés compuesto del r% anual, durante n años, obtendrás un capital final de

C_n=C_0(1+r/100)^n

Si fuéramos inmortales, ingresa un euro en el banco a un interés anual del 100% (si cuela) y échate a dormir.

Se dice, se cuenta, que una vez alguien le preguntó a Einstein cuál era la octava maravilla del mundo a lo que Einstein respondió “el interés compuesto».

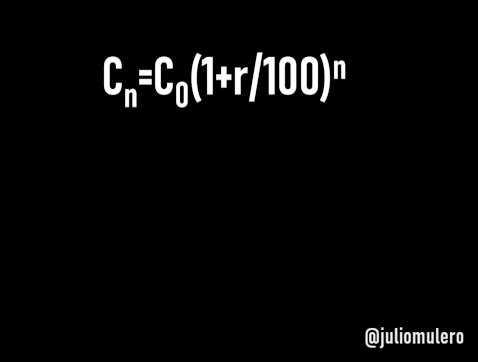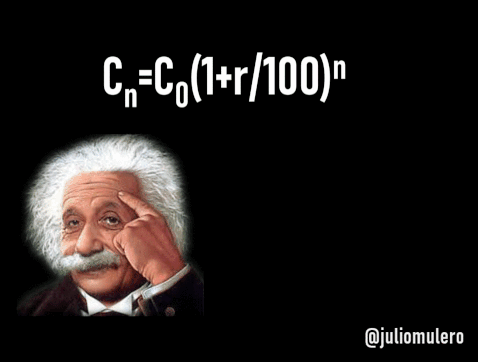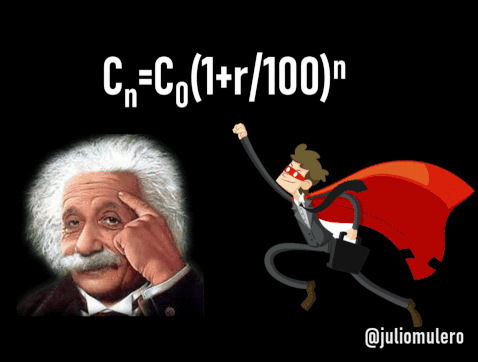
Bueno, ok. Hasta aquí de acuerdo.

Ahora imagina que queremos acortar el periodo de capitalización. Por ejemplo, supongamos que acordamos recibir intereses cada trimestre. Esto quiere decir que recibiremos el 25% de intereses cada trimestre (100%/4 trimestres).

Al finalizar el primer trimestre, dispondremos de 1.25€. Al finalizar el segundo, apróximadamente 1.56€. Al finalizar el tercero, 1.95€ (apróx.).

Resulta que tras un año (tras cuatro trimestres) tendremos 2.44€ (apróx.) que es más que lo que recibiríamos con un solo pago del 100%.

Como parece que nos ha ido bien reduciendo el periodo de capitalización, informamos al banco de que queremos que nos paguen cada día. Tras 365 pagos con un interés de 100/365%, acabaremos el año con 2.7145€ (apróx.).

Wow, esto es un chollo. A menor tiempo, más intereses.

¿Qué pasa entonces si decidimos hacer un pago de intereses “continuo”? ¿Qué pasa si dividimos el año en “infinitos” momentos de tiempo?

Vale, sí, ya sé que esto es físicamente imposible, pero ¿y si pudiéramos?

El capital final sería lim_{n->infity} (1+1/n)^n.

Este límite, cuyo valor es e, fue precisamente el que llamó la atención de Jacob Bernoulli. Este límite vale e.

Es decir, tus ingresos no crecerán indefinidamente… ¿Tú no prefieres π a e? Pues aquí tienes lo tienes, poniendo límite a tus caprichosos deseos. Donde las dan, las toman.

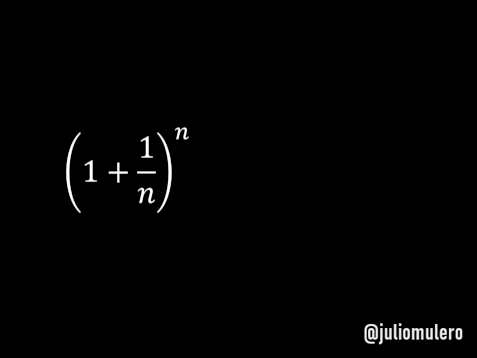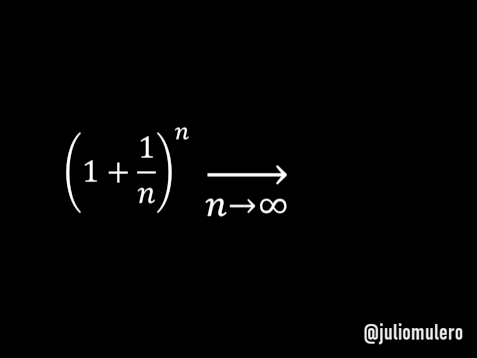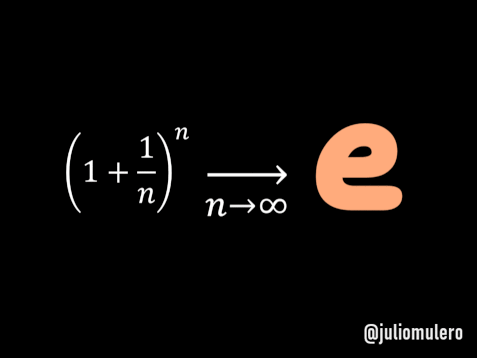
Siete años después, Leibniz escribió una carta a Huygens donde, por fin, el valor de e era reconocido (aunque fue llamado b). Fue Euler quién le llamó e (ya sea por la inicial de su nombre o simplemente porque la primera vocal ya estaba siendo usada) en una carta a Goldbach en 1731.

Ingenieros, biólogos, físicos, químicos, matemáticos, paleontólogos, médicos, estadísticos, financieros (as):

Hoy es el #DíaDeE.