Abrí los ojos sobre las tres de la mañana. Era una situación habitual y entonces solía ponerme de lado, agarrarme a la almohada y tratar de continuar durmiendo.
Pero aquel día no era como los demás, era #Halloween y las paradojas andaban sueltas.
#EnHebrasMatemáticas #Halloween #CarnaMatX5

El paseo por la casa del horror matemático había sido fructífero. Un rato de risas entre amigos. Un té. Una shisha. Y a la cama. Lo normal, vaya.
Sin embargo, cuando aquella noche abrí los ojos, una silueta oscura me miraba fijamente desde la puerta.

Palpé torpemente la mesilla de noche en busca de mis gafas y, cuando por fin pude ver claramente, aquella sombra había desaparecido.
Tras unos segundos de incredulidad, escuché una respiración entrecortada y una mano recorriendo mi espalda.

[Paradojas]Una paradoja es algo que a primera vista parece ser falso pero que en realidad es cierto; o que parece ser cierto pero que en rigor es falso; o sencillamente que encierra en sí mismo contradicciones.Las paradojas dependen del grado de desarrollo de las matemáticas en un momento dado; parodiando a Hamlet puede decirse que «lo que una vez fue paradoja, ya no lo es, pero puede volver a serlo».Las matemáticas encuentran en sus paradojas un camino para originar las más bellas y profundas teorías:«El testamento de la ciencia es un flujo continuo, de tal manera que la herejía del pasado es el evangelio del presente y el fundamento del mañana” (Kasner, et al., 1979).
Como si de un resorte se tratara, me destapé, di un salto y salí inmediatamente de la habitación.
El terror recorrió todo mi cuerpo al observar el enorme pasaje de 100 o 200 metros -qué se yo- donde hasta ayer mismo había una estancia que daba a la cocina y el baño.
Y, al final, una luz chispeante.

Lo que aquello fuera se levantó de la cama y oí un crujido de pasos sobre la tarima.
Así que, sin pensarlo demasiado, emprendí una huida desesperada por la estrechez de aquel oscuro pasillo.

[Zenón y la inconmesurabilidad]
Uno de los temas de mayor controversia entre los griegos fue el relativo a la relación que existe entre lo discreto y lo continuo. Este problema fue puesto en evidencia por el más destacado discípulo de Parménides, Zenón de Elea.
Según Proclo, Zenón planteó un total de cuarenta paradojas dedicadas principalmente al problema del continuo y a las relaciones entre espacio, tiempo y movimiento.
Nueve de dichas paradojas son descritas en la Física de Aristóteles y son esencialmente equivalentes entre sí. Aristóteles ofreció una refutación de algunas de ellas. En esta pesadilla fui “sorprendido” por tres de las más conocidas.
Las paradojas de Zenón emergen del supuesto de que “si una magnitud puede ser dividida entonces, a menudo, puede serlo indefinidamente”. Además, Zenón también supone que una cosa que no tiene magnitud no puede existir.
Sus razonamientos, ajenos sin embargo a toda posible matematización, constituyen el testimonio más antiguo que se conserva del pensamiento infinitesimal que nacerá de la mano de Leibniz y Newton en 1666.
Recorrí galopando la mitad del camino, y la mitad de la mitad, y la mitad de la mitad de la mitad, y, aunque me encontraba cada vez más y más cerca, no fui capaz de alcanzarla.

[Paradoja de la dicotomía]
Imagina que Zenón debe recorrer el espacio entre su casa y el parque. Para ello, deberá alcanzar en primer lugar el punto medio del trayecto;, después, el punto medio entre este último y la salida; y así sucesivamente.
Dado que nuestra vida es finita, “nadie puede completar un número infinito de tareas”, y es imposible que Zenón llegue al parque.
El razonamiento de Zenón es razonable (valga la redundancia), pero es claramente contrario a la experiencia. ¿Cómo no va a llegar nunca a un punto que está fijo? ¿Acaso el movimiento no existe?
¿Cuáles son las ideas formales que dan lugar a esta conclusión?
- Desplazarse de un punto A hasta un punto B es una tarea formada por un número infinito de tareas menores.
- Es lógicamente imposible completar una serie infinita de tareas discretas.
Lo cierto es que este simple hecho, relacionado con la posibilidad “real” de dividir el espacio en un número infinito de sumandos, se “desmiente” fácilmente gracias a las matemáticas.
Y, en consonancia con la experiencia, Zenón llegará al parque sin lugar a dudas.
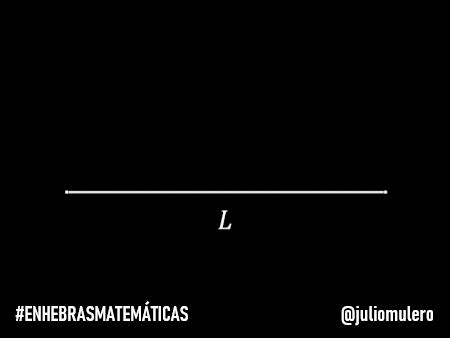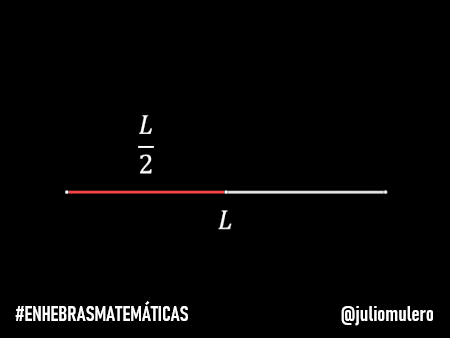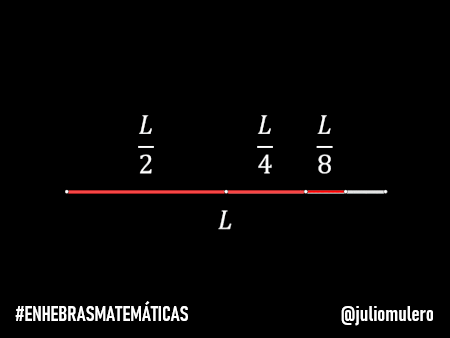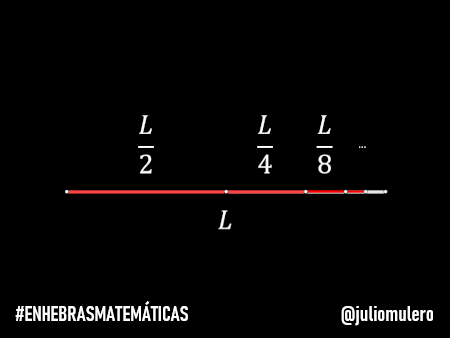
Supongamos que la distancia a recorrer es L. Entonces las distancias recorridas serán L/2 (la mitad), L/4 (la mitad de la mitad), L/8 (la mitad de la mitad de la mitad)…
Estas cantidades resultan ser los términos de una progresión geométrica de razón ½, es decir, cada término se obtiene multiplicando el anterior por ½, y la distancia total será:
L/2+L/4+L/8+…
Si dicha razón es menor que uno (como es nuestro caso) es fácil demostrar que la suma de los infinitos términos de la progresión se obtiene mediante la fórmula S = a₁/(1 – r), donde a₁ es el primero de los términos.
En el fondo, el error está en presuponer que la suma de infinitas cantidades, ya sean espacios o tiempos, debe ser una cantidad infinita.
El cansancio pudo conmigo y me desvanecí. De repente, recuperé la consciencia al sentir un cuerpo sobre el mío, como si un perro me olisqueara el cuello y las orejas.
¿Por qué huyes de mí, muchacho?, me dijo con la voz rota y su boca pegada a mi oreja.

El frío del pasillo contrastaba con la vieja y caliente humedad de sus respiraciones.
Presa del miedo, abrí los ojos, giré la cabeza lentamente y, rodeado de tinieblas, encontré una cara cercenada por las arrugas.

El anciano, que parecía deshacerse en leves convulsiones, me miraba fijamente a escasos diez centímetros. Extendió un dedo descarnado, lo posó en mi barbilla, y me hizo levantar la mirada.
Vamos adentro, me dijo con una voz ronca.

Se levantó y comenzó a dar pasos hacia el portal. Estaba desnudo y toda la piel de la parte superior del espectro descansaba, cedida, sobre la parte baja de su espalda.

Yo que me había incorporado y me apoyaba, abrazando mis piernas, sobre la pared, no tenía ninguna intención de seguirle, pero de repente se paró, sus miembros se desencajaron, se lanzaron hacia mí y me pusieron en pie. Camina, insistió.

Me llevaba unos diez metros de ventaja y una fuerza oscura me incitaba a avanzar. A su paso iba dejando un olor nauseabundo y un calor extraño que me descongelaba los huesos.

Mi ritmo era ciertamente mayor que el suyo, pero, cuando hube recorrido la ventaja inicial, el anciano se encontraba unos metros más adelante. Y cuando los hube transitado, me llevaba unos pocos metros más.

[Paradoja de Aquiles y la Tortuga]
Aquiles y la tortuga es, quizás, la más conocida de las paradojas de Zenón.
En ella, Aquiles, el atleta más veloz, capaz de alcanzar los 100 m/s, se enfrenta a una tortuga en una “disputadísima” carrera. A fin de no parecer un engreído, Aquiles le concede una considerable ventaja (100 metros).
En solo 10 segundos, Aquiles recorre la ventaja que le separa de la tortuga, y esta, que avanza a 1 m/s, se ha desplazado 10 metros. En un solo segundo, Aquiles recorre esos 10 metros, la tortuga se ha desplazado 1 metro; cuando Aquiles recorre ese metro, la tortuga ha avanzado 10 cm…
Según Zenón, es imposible que Aquiles alcance a la tortuga puesto que debería cubrir infinitos trayectos, recorrer un espacio infinito y emplear un tiempo infinito. La tortuga se hace con el triunfo.
¿Cuáles son las ideas formales que dan lugar a esta conclusión?
- Para que un cuerpo en movimiento alcance a otro, también en movimiento, es preciso que el primero pase antes por cada uno de los puntos que el otro va dejando.
- El cuerpo perseguidor tiene que completar una serie infinita de tareas antes de alcanzar al perseguido.
En el razonamiento de Zenón aparece, de nuevo, el hecho de que la suma de infinitas distancias será infinito y Aquiles necesitaría un tiempo infinito.
Y la suma de los infinitos términos de una progresión geométrica decreciente) nos permite comprobar que, con las velocidades anteriormente indicadas, el tiempo empleado por Aquiles hasta alcanzar a la tortuga será de 11.1111… segundos. Menos de 12 segundos, vaya (y ya me parece mucho).
Bajo una apariencia “inofensiva” esta paradoja fue uno de los caballos de batalla de las matemáticas durante muchos siglos. De hecho, se tardó más de 2000 años en desvelar el enigma por completo, gracias a la Teoría de Límites y el Cálculo Infinitesimal.
Las firmes paredes comenzaron entonces a estrecharse más y más sobre mi cuerpo. Los huesos de mi espalda, de mis hombros, de mis piernas incluso, ya eran añicos y, de repente vi un ojo blanco en el angosto agujero en que se había convertido el pasillo.

Grité. Y todo se hizo oscuridad. Sin sensación física alguna, mi alma era un punto que volaba por un vacío negro, así como una mota de polvo, en un movimiento volátil. Espeso. Curvilíneo.

Entonces unos fogonazos de luz empezaron a calcinarme la visión. Y, entre las llamaradas, apareció la misma sombra. Una sombra que, aun sin moverse, parecía estar más y más cerca.
[Paradoja de la flecha]

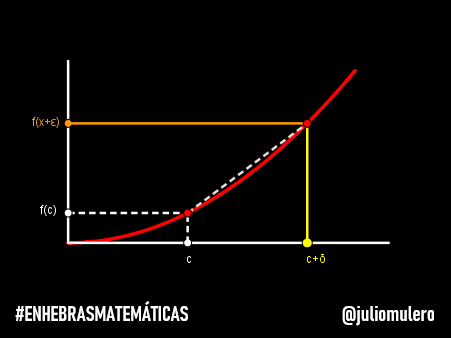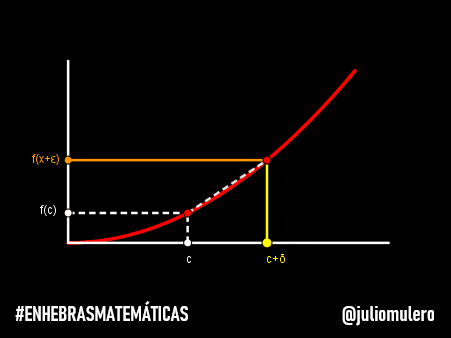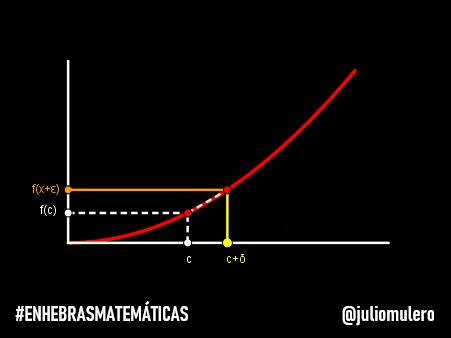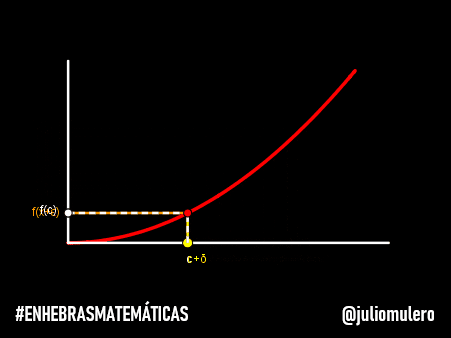
Imagina que se lanza se lanza una flecha. En cada momento de tiempo, la flecha está en una posición específica, y si ese momento es lo suficientemente pequeño, la flecha no tiene tiempo para moverse.
Es decir, la flecha está en reposo durante ese instante.
Ahora bien, el mismo argumento puede aplicarse a los demás periodos de tiempo, de modo que la flecha está siempre en reposo.
¿Cuáles son las ideas formales que dan lugar a esta conclusión?
- En cada instante ti, la flecha no se mueve,
- Un intervalo de tiempo no es más que una colección de instantes t₀,t₁,…tᵢ,…,
En el fondo, lo que aquí está ocurriendo es que un instante no es suficientemente grande para que el movimiento tenga lugar, ya que el movimiento es una relación entre objetos, lugares y varios instantes.
Un objeto está en reposo en un instante justo cuando permanece en la misma posición en todos los instantes cercanos, y está en movimiento en un instante si “vive” en distintos sitios en instantes cercanos.
Sin posibilidad alguna de escapar, con el pánico picoteándome las entrañas, el corazón vacío de sangre y los pulmones inundados de un miedo venenoso, cerré los ojos tan fuerte como pude. Y me dispuse a poner el punto final.

Pero entonces un sonido estridente me reventó los oídos. Me incorporé y comprobé que todo había sido una pesadilla. Una pesadilla de esas que se recuerdan en #Halloween.

Si has leído hasta aquí, muchísimas gracias. Las paradojas a veces pueden convertirse en auténticos laberintos para la razón.
Esta publicación participa en el #CarnaMatX5 cuyo anfitrión es @gaussianos (https://www.gaussianos.com/), continua inspiración para todos aquellos que amamos las matemáticas.